Table of Contents

• 1  Data Description
• 2  Imports
• 3  Useful Scripts
• 4  Load the data
• 5  descriptive statistics
  • 5.1  Mean
  • 5.2  standard deviation
  • 5.3  skewness
  • 5.4  kurtosis
• 6  Robust statistics: median
• 7  Outliers
• 8  Mutual Information between Target and the Predictors

Kernel Author:
Bhishan Poudel, Ph.D Astrophysics .

Data Description

The datasets contains transactions made by credit cards in September 2013 by european cardholders.

This dataset presents transactions that occurred in two days, where we have 492 frauds out of 284,807 transactions.

The dataset is highly unbalanced, the positive class (frauds) account for 0.172% of all transactions.

It contains only numerical input variables which are the result of a PCA transformation.

Unfortunately, due to confidentiality issues, we cannot provide the original features and more background information about the data.

Features V1, V2, ... V28 are the principal components obtained with PCA, the only features which have not been transformed with PCA are 'Time' and 'Amount'.

Feature 'Time' contains the seconds elapsed between each transaction and the first transaction in the dataset. The feature 'Amount' is the transaction Amount, this feature can be used for example-dependant cost-senstive learning.

Feature 'Class' is the response variable and it takes value 1 in case of fraud and 0 otherwise.

Imports

import numpy as np
import pandas as pd
import seaborn as sns
sns.set(color_codes=True)

import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

import os
import time

# random state
SEED = 0
RNG = np.random.RandomState(SEED)

# Jupyter notebook settings for pandas
pd.set_option('display.max_columns', 200)
pd.set_option('display.max_rows', 100) # None for all the rows
pd.set_option('display.max_colwidth', 50)

print([(x.__name__,x.__version__) for x in [np, pd,sns,matplotlib]])

[('numpy', '1.16.4'), ('pandas', '0.25.0'), ('seaborn', '0.9.0'), ('matplotlib', '3.1.1')]

import scipy
from scipy import stats

import IPython
from IPython.display import display

from sklearn.preprocessing import MinMaxScaler, StandardScaler, RobustScaler

Useful Scripts

def show_method_attributes(method, ncols=7):
    """ Show all the attributes of a given method.
    Example:
    ========
    show_method_attributes(list)
     """
    x = [i for i in dir(method) if i[0].islower()]
    x = [i for i in x if i not in 'os np pd sys time psycopg2'.split()]

    return pd.DataFrame(np.array_split(x,ncols)).T.fillna('')

def json_dump_tofile(myjson,ofile,sort_keys=False):
    """Write json dictionary to a datafile.
    
    Usage:
    myjson = {'num': 5, my_list = [1,2,'apple']}
    json_dump_tofile(myjson, ofile)
    
    """
    import io
    import json

    with io.open(ofile, 'w', encoding='utf8') as fo:
        json_str = json.dumps(myjson,
                          indent=4,
                          sort_keys=sort_keys,
                          separators=(',', ': '),
                          ensure_ascii=False)
        fo.write(str(json_str))

Load the data

df = pd.read_csv('../data/raw/creditcard.csv.zip',compression='zip')
print(df.shape)
df.head()

(284807, 31)

	Time	V1	V2	V3	V4	V5	V6	V7	V8	V9	V10	V11	V12	V13	V14	V15	V16	V17	V18	V19	V20	V21	V22	V23	V24	V25	V26	V27	V28	Amount	Class
0	0.0	-1.359807	-0.072781	2.536347	1.378155	-0.338321	0.462388	0.239599	0.098698	0.363787	0.090794	-0.551600	-0.617801	-0.991390	-0.311169	1.468177	-0.470401	0.207971	0.025791	0.403993	0.251412	-0.018307	0.277838	-0.110474	0.066928	0.128539	-0.189115	0.133558	-0.021053	149.62	0
1	0.0	1.191857	0.266151	0.166480	0.448154	0.060018	-0.082361	-0.078803	0.085102	-0.255425	-0.166974	1.612727	1.065235	0.489095	-0.143772	0.635558	0.463917	-0.114805	-0.183361	-0.145783	-0.069083	-0.225775	-0.638672	0.101288	-0.339846	0.167170	0.125895	-0.008983	0.014724	2.69	0
2	1.0	-1.358354	-1.340163	1.773209	0.379780	-0.503198	1.800499	0.791461	0.247676	-1.514654	0.207643	0.624501	0.066084	0.717293	-0.165946	2.345865	-2.890083	1.109969	-0.121359	-2.261857	0.524980	0.247998	0.771679	0.909412	-0.689281	-0.327642	-0.139097	-0.055353	-0.059752	378.66	0
3	1.0	-0.966272	-0.185226	1.792993	-0.863291	-0.010309	1.247203	0.237609	0.377436	-1.387024	-0.054952	-0.226487	0.178228	0.507757	-0.287924	-0.631418	-1.059647	-0.684093	1.965775	-1.232622	-0.208038	-0.108300	0.005274	-0.190321	-1.175575	0.647376	-0.221929	0.062723	0.061458	123.50	0
4	2.0	-1.158233	0.877737	1.548718	0.403034	-0.407193	0.095921	0.592941	-0.270533	0.817739	0.753074	-0.822843	0.538196	1.345852	-1.119670	0.175121	-0.451449	-0.237033	-0.038195	0.803487	0.408542	-0.009431	0.798278	-0.137458	0.141267	-0.206010	0.502292	0.219422	0.215153	69.99	0

df.filter(regex='V').columns

Index(['V1', 'V2', 'V3', 'V4', 'V5', 'V6', 'V7', 'V8', 'V9', 'V10', 'V11',
       'V12', 'V13', 'V14', 'V15', 'V16', 'V17', 'V18', 'V19', 'V20', 'V21',
       'V22', 'V23', 'V24', 'V25', 'V26', 'V27', 'V28'],
      dtype='object')

descriptive statistics

pca_vars = ['V%i' % k for k in range(1,29)]
df[pca_vars].describe()

	V1	V2	V3	V4	V5	V6	V7	V8	V9	V10	V11	V12	V13	V14	V15	V16	V17	V18	V19	V20	V21	V22	V23	V24	V25	V26	V27	V28
count	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05	2.848070e+05
mean	1.165980e-15	3.416908e-16	-1.373150e-15	2.086869e-15	9.604066e-16	1.490107e-15	-5.556467e-16	1.177556e-16	-2.406455e-15	2.239751e-15	1.673327e-15	-1.254995e-15	8.176030e-16	1.206296e-15	4.913003e-15	1.437666e-15	-3.800113e-16	9.572133e-16	1.039817e-15	6.406703e-16	1.656562e-16	-3.444850e-16	2.578648e-16	4.471968e-15	5.340915e-16	1.687098e-15	-3.666453e-16	-1.220404e-16
std	1.958696e+00	1.651309e+00	1.516255e+00	1.415869e+00	1.380247e+00	1.332271e+00	1.237094e+00	1.194353e+00	1.098632e+00	1.088850e+00	1.020713e+00	9.992014e-01	9.952742e-01	9.585956e-01	9.153160e-01	8.762529e-01	8.493371e-01	8.381762e-01	8.140405e-01	7.709250e-01	7.345240e-01	7.257016e-01	6.244603e-01	6.056471e-01	5.212781e-01	4.822270e-01	4.036325e-01	3.300833e-01
min	-5.640751e+01	-7.271573e+01	-4.832559e+01	-5.683171e+00	-1.137433e+02	-2.616051e+01	-4.355724e+01	-7.321672e+01	-1.343407e+01	-2.458826e+01	-4.797473e+00	-1.868371e+01	-5.791881e+00	-1.921433e+01	-4.498945e+00	-1.412985e+01	-2.516280e+01	-9.498746e+00	-7.213527e+00	-5.449772e+01	-3.483038e+01	-1.093314e+01	-4.480774e+01	-2.836627e+00	-1.029540e+01	-2.604551e+00	-2.256568e+01	-1.543008e+01
25%	-9.203734e-01	-5.985499e-01	-8.903648e-01	-8.486401e-01	-6.915971e-01	-7.682956e-01	-5.540759e-01	-2.086297e-01	-6.430976e-01	-5.354257e-01	-7.624942e-01	-4.055715e-01	-6.485393e-01	-4.255740e-01	-5.828843e-01	-4.680368e-01	-4.837483e-01	-4.988498e-01	-4.562989e-01	-2.117214e-01	-2.283949e-01	-5.423504e-01	-1.618463e-01	-3.545861e-01	-3.171451e-01	-3.269839e-01	-7.083953e-02	-5.295979e-02
50%	1.810880e-02	6.548556e-02	1.798463e-01	-1.984653e-02	-5.433583e-02	-2.741871e-01	4.010308e-02	2.235804e-02	-5.142873e-02	-9.291738e-02	-3.275735e-02	1.400326e-01	-1.356806e-02	5.060132e-02	4.807155e-02	6.641332e-02	-6.567575e-02	-3.636312e-03	3.734823e-03	-6.248109e-02	-2.945017e-02	6.781943e-03	-1.119293e-02	4.097606e-02	1.659350e-02	-5.213911e-02	1.342146e-03	1.124383e-02
75%	1.315642e+00	8.037239e-01	1.027196e+00	7.433413e-01	6.119264e-01	3.985649e-01	5.704361e-01	3.273459e-01	5.971390e-01	4.539234e-01	7.395934e-01	6.182380e-01	6.625050e-01	4.931498e-01	6.488208e-01	5.232963e-01	3.996750e-01	5.008067e-01	4.589494e-01	1.330408e-01	1.863772e-01	5.285536e-01	1.476421e-01	4.395266e-01	3.507156e-01	2.409522e-01	9.104512e-02	7.827995e-02
max	2.454930e+00	2.205773e+01	9.382558e+00	1.687534e+01	3.480167e+01	7.330163e+01	1.205895e+02	2.000721e+01	1.559499e+01	2.374514e+01	1.201891e+01	7.848392e+00	7.126883e+00	1.052677e+01	8.877742e+00	1.731511e+01	9.253526e+00	5.041069e+00	5.591971e+00	3.942090e+01	2.720284e+01	1.050309e+01	2.252841e+01	4.584549e+00	7.519589e+00	3.517346e+00	3.161220e+01	3.384781e+01

Mean

def plot_statistics(df,features,statistic,color='b'):
    plt.figure(figsize=(12,4), dpi=80)
    sns.barplot(x=features, y= df[pca_vars].agg(statistic),color=color)
    plt.xlabel('Features')
    plt.ylabel(statistic.title())
    plt.title(statistic.title()+ ' for all features')
    plt.savefig(f'../reports/statistics/{statistic}.png',dpi=300)
    plt.show()
    plt.close()

plot_statistics(df,pca_vars,'mean',color='b')
# all means are zero

standard deviation

plot_statistics(df,pca_vars,'std',color='tomato')

# NOTE that we have PCA selected variables and variables have decreasing variance.
# all std are less than 2.0

skewness

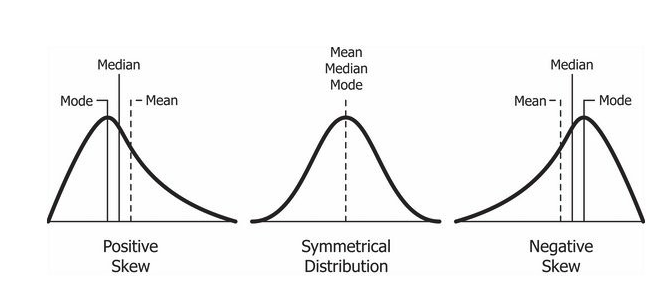
plot_statistics(df,pca_vars,'skew',color='seagreen')

# top point is always mode
# also, we have mean median mode (the order does not change, but <> changes.)
# for +ve skew, mean > median > mode
# for -ve skew, mean < median < mode
# some features are skewed eg. V8, V23, V28

df['V28'].skew()

11.192091192212809

plt.figure(figsize=(12,4), dpi=80)
sns.distplot(df['V28'], bins=300, kde=False)
plt.ylabel('Count')
plt.title(' distribution plot of feature: V28')

# almost all of data is centered around 0.

Text(0.5, 1.0, ' distribution plot of feature: V28')

plt.figure(figsize=(12,4), dpi=80)
sns.distplot(df['V28'], bins=3000, kde=False)
plt.ylabel('Count')
plt.title(' distribution plot of feature: V28 with selected x limit')
plt.xlim(-2,2)

# almost all of data is centered around 0.

(-2, 2)

plt.figure(figsize=(12,4), dpi=80)
sns.boxplot(df['V28'])
plt.title('Box plot of feature: V28')
plt.savefig('../reports/statistics/v28_boxplot.png',dpi=300)

# there are so many outliers
# boxplot is hard to read, we can plot kurtosis plot.

kurtosis

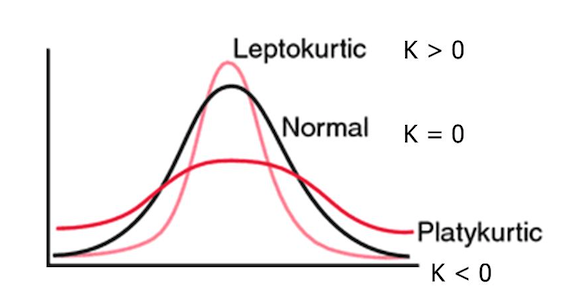
plot_statistics(df,pca_vars,'kurtosis',color='darkorange')

df['V28'].kurtosis()

933.3975020960183

Robust statistics: median

# pca variables are heavily tailed, we can use more robust descriptive
# statistic such as median.

plot_statistics(df,pca_vars,'median',color='b')

# medians are roughly 0

plt.figure(figsize=(12,4), dpi=80)
sns.barplot(x=pca_vars, y=df[pca_vars].quantile(0.75)
            - df[pca_vars].quantile(0.25), color='darkred')
plt.xlabel('Column')
plt.ylabel('IQR')
plt.title('V1-V28 IQRs')
plt.savefig('../reports/statistics/iqr.png',dpi=300)

plot_statistics(df,pca_vars,'std',color='darkred')
# IQR and standard deviations look very similar.
# this means not too many points are outliers.

Outliers

plt.figure(figsize=(12,8))
ax = sns.boxplot(data = df.drop(columns=['Amount', 'Class', 'Time']), 
  orient = 'h', palette = 'winter')

ax.set(xlim=(-5,5))
ax.set_facecolor('#fafafa')
ax.set_title('Box plots of features V1 to V28')
ax.set_ylabel('Variables')
plt.savefig('../reports/statistics/boxplot_all_features.png',dpi=300)

Mutual Information between Target and the Predictors

from sklearn.feature_selection import mutual_info_classif

%%time
mutual_infos = pd.Series(data=mutual_info_classif(df[pca_vars], df['Class'],
                                                  discrete_features=False,
                                                  random_state=random_state),
                         index=pca_vars)

CPU times: user 1min 20s, sys: 1.33 s, total: 1min 21s
Wall time: 1min 23s

mutual_infos.sort_values(ascending=False).to_frame().T

# most related quantites are v17, v14, v12 and so on.

	V17	V14	V12	V10	V11	V16	V4	V3	V18	V9	V7	V2	V21	V27	V5	V6	V1	V8	V28	V19	V20	V23	V24	V26	V25	V13	V22	V15
0	0.008258	0.008136	0.007601	0.00753	0.006831	0.006144	0.004976	0.004952	0.004317	0.004277	0.003952	0.003228	0.002452	0.002444	0.002391	0.002388	0.002127	0.001898	0.001871	0.001472	0.001207	0.000762	0.000642	0.0005	0.000498	0.000408	0.000353	0.000315